보로노이다이어그램, 어려운 수학을 재밌게 만드는 법

 

기린의 얼룩무늬나 잠자리 날개의 그물 같은 모양을 보며 "이건 누가 그렸을까?"라고 궁금해한 적이 있으신가요? 수학이라고 하면 머리 아픈 공식과 계산만 떠올리게 마련입니다. 하지만 우리 주변의 자연과 세상은 아주 흥미로운 기하학적 원리로 이루어져 있습니다. 수학을 싫어하는 아이들에게 흥미를 불어넣고 싶은 부모님이나 선생님이라면 오늘 이야기에 주목해 주세요.

결론부터 말씀드리자면, '보로노이 다이어그램'은 점과 점 사이의 거리를 이용해 가장 공평한 영역을 나누는 방법입니다. 거창한 이름과 달리 원리는 아주 단순합니다. 오늘 이 글을 통해 딱딱한 교과서 공부가 아니라, 그림을 그리고 종이를 접으며 노는 즐거운 예술 활동으로 기하학을 배우는 비법을 초등학생도 이해하기 쉽게 알려드리겠습니다.

 

자연 속 숨겨진 모자이크 무늬 찾기

 

거북이 등껍질이나 가뭄에 갈라진 논바닥을 자세히 들여다보면 신기하게도 비슷한 다각형 모양들이 빼곡히 채워져 있는 것을 볼 수 있습니다. 이것은 자연이 스스로 가장 효율적이고 튼튼한 구조를 만들기 위해 선택한 결과물입니다. 이 무늬들은 무작위로 생긴 것이 아니라, 각 중심점에서 가장 가까운 거리에 있는 영역들이 만나서 생긴 경계선입니다.

아이들에게 이 개념을 설명할 때는 밖으로 나가 자연 관찰을 하는 것이 최고의 해결책입니다. 나뭇잎의 잎맥이나 옥수수 알갱이의 배열을 보며 "이 구역의 주인은 누구일까?"라고 질문을 던져보세요. 자연스럽게 자기 영역을 지키려는 힘들이 만나 균형을 이룬 모습이라는 것을 깨닫게 해주면, 수학이 책 속에만 있는 지루한 학문이 아니라는 사실을 알게 됩니다.

 

피자 배달 구역으로 배우는 공평함

 

이 도형의 원리를 가장 쉽게 이해하는 방법은 '땅따먹기'나 '배달 구역 정하기' 게임을 하는 것입니다. 예를 들어 우리 동네에 피자 가게가 세 군데 있다고 상상해 봅시다. 사람들은 배가 고프니 무조건 가장 가까운 가게에서 시켜 먹으려고 할 것입니다. 그렇다면 지도 위에 가게 위치를 점으로 찍고, 각 가게가 담당해야 할 구역을 어떻게 나누면 좋을까요?

지도를 펼쳐 놓고 가게(점) 사이를 연결한 선의 딱 중간을 수직으로 가로지르는 선을 그어보세요. 이렇게 하면 각 지점에서 가장 가까운 영역이 마법처럼 나누어집니다. 내 집이 어느 구역에 속하는지 눈으로 확인하는 과정에서 '수직이등분선'이라는 어려운 용어 대신, 거리를 똑같이 나누는 '공평한 선'이라는 개념을 자연스럽게 익힐 수 있습니다.

 

종이 접기로 완성하는 기하학 미술

 

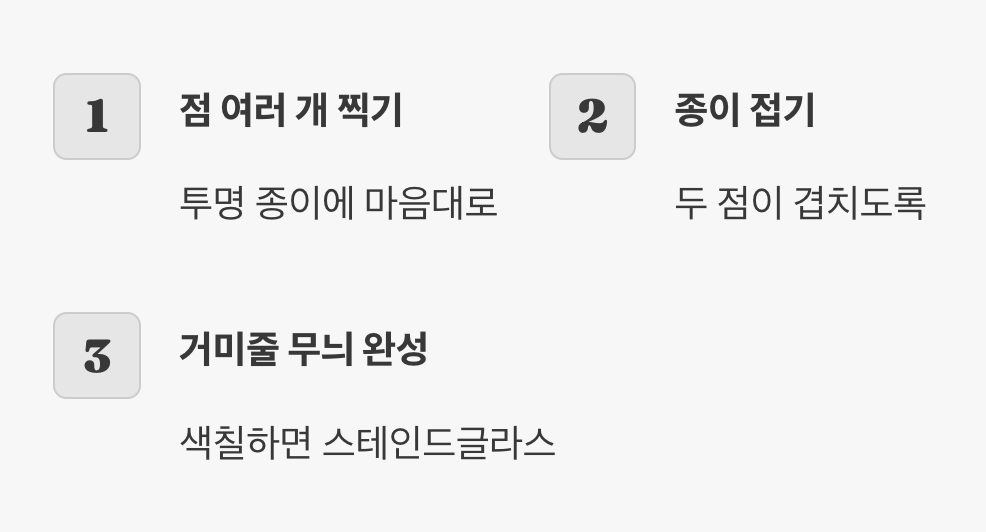
자와 컴퍼스를 사용해 작도하는 것은 어린 학생들에게 너무 어렵고 지루할 수 있습니다. 대신 투명한 종이와 사인펜을 이용한 '종이 접기' 놀이를 추천합니다. 종이 위에 점을 여러 개 마음대로 찍은 뒤, 두 점이 서로 겹쳐지도록 종이를 접었다가 펼쳐보세요. 그러면 두 점 사이의 접힌 자국이 생기는데, 이 선이 바로 경계선이 됩니다.

모든 점이 서로 만나도록 이리저리 접다 보면 어느새 멋진 거미줄 같은 무늬가 완성됩니다. 이 활동은 손을 직접 움직이며 도형의 성질을 체득하게 해주는 훌륭한 해결책입니다. 완성된 칸마다 서로 다른 색깔을 칠하면 스테인드글라스처럼 아름다운 작품이 탄생합니다. 수학 시간이 미술 시간으로 변하는 순간, 아이들의 눈빛이 달라질 것입니다.

 

휴대폰이 잘 터지는 과학적 비밀

 

우리가 매일 쓰는 스마트폰이나 내비게이션에도 이 원리가 숨어 있습니다. 이동통신사는 기지국을 어디에 세워야 전파가 겹치지 않고 효율적으로 도시 전체를 커버할 수 있을지 고민합니다. 이때 바로 이 다이어그램을 활용해 기지국 하나가 담당할 구역을 결정합니다.

아이들에게 "네가 게임을 끊김 없이 할 수 있는 건 이 수학 원리 덕분이야"라고 이야기해 주세요. 추상적인 도형이 내 생활의 편리함을 만들어준다는 것을 알면 공부해야 할 이유를 찾게 됩니다. 복잡한 도시 설계를 단순한 점과 선으로 해결하는 과정을 보여주는 것은 과학적 사고력을 키워주는 좋은 방법입니다.

 

건축과 디자인으로 확장하는 사고력

 

세계적인 건축물 중에는 이 패턴을 활용해 지은 것들이 많습니다. 베이징 올림픽 수영 경기장인 '워터큐브'가 대표적입니다. 비누 거품이 모여 있는 모양을 본떠 만든 이 건물은 튼튼하면서도 아름답습니다. 단순히 평면에 그리는 것을 넘어 입체적인 구조물로 상상력을 넓혀주는 것이 중요합니다.

주변에서 찾을 수 있는 보도블록이나 포장지 무늬에서도 비슷한 패턴을 찾아보세요. 그리고 아이와 함께 빨대나 수수깡을 이용해 직접 입체 구조물을 만들어보는 것도 좋습니다. 평면에서 배운 원리를 공간으로 확장하면서 창의적인 문제 해결 능력을 기를 수 있습니다.

 

자주 묻는 질문 (FAQ)

 

Q. 이 이론은 누가 처음 발견했나요?
A. 러시아의 수학자 '조지 보로노이'가 정립했습니다. 물론 그전에도 데카르트 같은 학자들이 비슷한 개념을 이야기했지만, 이를 일반화하고 체계적으로 정리하여 자신의 이름을 딴 다이어그램으로 세상에 알린 사람은 보로노이입니다.

 

Q. 잠자리 날개 말고 또 어디서 볼 수 있나요?
A. 기린의 얼룩무늬, 표범의 무늬, 마른 땅이 갈라지는 모습, 그리고 현미경으로 본 우리 몸의 세포 모양에서도 발견할 수 있습니다. 3D 프린팅 기술이나 로봇이 장애물을 피해 가는 경로를 짤 때도 이 원리가 아주 중요하게 쓰입니다.

 

Q. 집에서 쉽게 할 수 있는 다른 놀이는 없나요?
A. 쿠키 반죽에 초코칩을 박아 놓고, 구워질 때 퍼지는 모양을 관찰하는 요리 놀이도 좋습니다. 혹은 비눗방울이 서로 맞닿아 생기는 막의 모양을 관찰하는 것도 아주 재미있는 실험이 됩니다.

 

보로노이 다이어그램 입문, 최소한의 개념과 용어 정리

보로노이 다이어그램 입문, 최소한의 개념과 용어 정리

보로노이다이어그램, 실생활에 어떻게 쓰일까? (놀라운 사례 4가지)

보로노이다이어그램, 실생활에 어떻게 쓰일까? (놀라운 사례 4가지)

초등학생도 이해하는 보로노이 다이어그램 이야기

초등학생도 이해하는 보로노이 다이어그램 이야기

 

추가 정보 및 도움이 되는 자료

• 보로노이 다이어그램 그리는 법
  인터랙티브 도구로 점 찍고 수직이등분선 그려 평면 분할 원리를 실습하며 이해합니다. 
• 보로노이 다이어그램 만들기(학생자료)
  학생용 활동지로 점 찍기·수직이등분선 그리기·파출소 관할구역 나누기로 재미있게 배웁니다. 
• [핫클립] 보로노이 다이어그램 만들기
  간단 재료로 기린 무늬·잠자리 날개 모방해 보로노이 다이어그램 제작하며 수학 원리 배웁니다. 
• 삼각형의 외심으로 보로노이 다이어그램을 그리자
  삼각형 외심 연결로 들로네 삼각분할과 연계해 보로노이 다이어그램 작도하는 교실 활동 소개합니다. 
• 무작위로 나눈 그림에도 이유가 있다! 보로노이 다이어그램
  자연 현상·콜레라 추적 사례 통해 보로노이 다이어그램의 실생활 적용을 흥미롭게 설명합니다.